[`BUAA-OO`] 第一单元：表达式展开

[toc]

概述

面向对象课第一单元的主题是表达式展开和化简，主要考察的内容是面向对象设计的思想，具体体现为表达式(Expr)，项(Term)等类的构建和它们的对象，方法的管理。第一单元共有三次迭代任务，分别是：

单变量单层括号的多项式展开
含有自定义递推函数，三角函数，多层括号的多项式展开和化简
含有自定义普通函数的多项式展开，求导和化简

客观来说，第一次作业由于是从零开始构建，难点主要在于理解递归下降的到底要做什么，以及怎么实现递归下降解析。第二次作业的难度和码量同步达到了巅峰，三角函数的引入改变了多项式最基本组成单元的形式，递推函数的引入大大增加了解析和计算的难度，多层括号可能意味着递归层数的加深。第三次作业的难点主要在于求导的设计。下面我们具体来回顾和总结第一单元的开发。

`UML`类图和度量分析

第一单元作业的类图如下：

OO_hw1

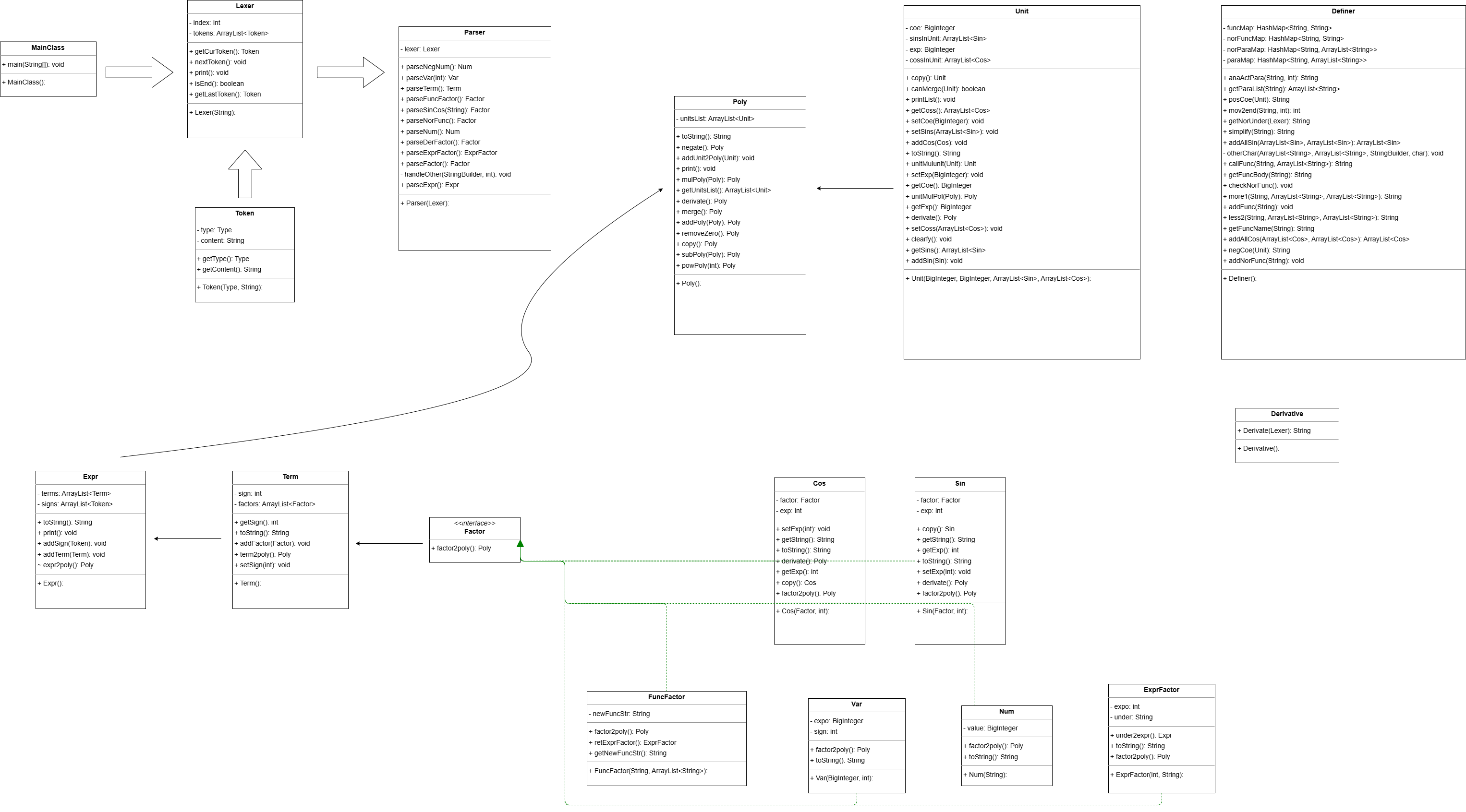
在本次作业中，我总共创建了17个类或接口的实现，共1600余行代码。在此具体解释一下每个类的设计考虑：

# 主类 负责简单的读入和输出
public class MainClass{}              

# 递归下降板块
public class Token{} 			// 词块  
public class Lexer{}			// 将输入字符串切成一个个词块
public class Parser{}			// 对lexer得到的词块进行解析，得到组成表达式的项的集合，组成项的因子集合
    
# 数据管理板块
public class Expr{}				// 表达式类
public class Term{}				// 项类
public Interface Factor{}		// 因子 
public class Sin implements Factor{}			// 正弦因子
public class Cos implements Factor{}			// 余弦因子
public class ExprFactor implements Factor{}		// 表达式因子
public class FuncFactor implements Factor{}		// 自定义函数因子
public class Var implements Factor{}		   // 幂函数因子 
public class Num implements Factor{}		   // 常数因子
public class Poly{}				// 多项式类
public class Unit{}              // 多项式组成单元
    
# 工具类
public class Definer{}           // 处理自定义函数相关问题的工具类
public class Derivative{}		// 处理求导相关问题的工具类

应该说，上述类和接口的设计都是很自然的，面向需求的。

MetrixReloaded复杂度统计如下：

OO_hw1

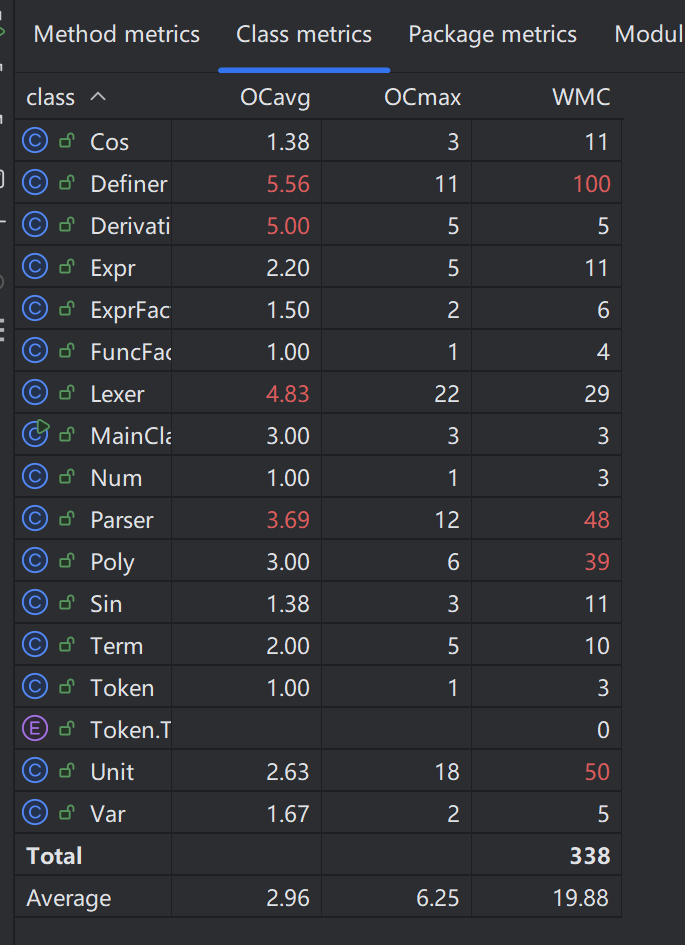
通过class metrix工具的分析可见，Definer和Derivative两个工具类的复杂度很高（OCavg均达到了5.00及以上），主要原因可能是：

实现自定义函数实参替换形参和多项式求导的一众方法分别放在了上述两个类中，类内方法之间有着复杂的相互调用关系，导致复杂度增高。
替换和求导后的式子往往并非最简，且它们可能成为三角函数或幂函数的组成部分，这就要求我们递归调用全局的方法对这些式子化简，导致复杂度增高。

第一次作业分析

简洁起见，我们在作业分析中只介绍思路概述和每次作业难点的处理。每次作业的具体分析见博主博客(https://jiangshiyi0822.github.io/)

思路概述

我们首先通过标准输入获得一个符合规范的表达式，并将其以String的类型传入lexer进行词法解析，获得一系列词块（token）。
然后我们利用递归下降的方法将token组合起来，自底向上形成一个个符合规范的factor，term，expression。
通过建立多项式类（Poly），单项式类（Mono）和实现它们的加，减，乘，幂运算方法来展开表达式。
最后还需要对输出结果做一定的化简。

语法解析（递归下降）

为了理解递归下降的最终目标，我们首先介绍表达式类（Expr），项类（Term），因子接口（Factor）。

public class Expr {
    private final ArrayList<Term> terms = new ArrayList<>();   // 对每个表达式维护一个项构成的列表
    private final ArrayList<Token> signs = new ArrayList<>();  // 对每个表达式维护一个项的符号的列表
}

public class Term {
    private int sign;  // 项的整体符号
    private final ArrayList<Factor> factors = new ArrayList<>();  // 项的因子构成的列表
}

1
2
3

public class Var implements Factor {}         // 幂函数因子
public class Num implements Factor {}         // 常数因子
public class ExprFactor implements Factor {}  // 表达式因子

我们进行语法解析的最终目的就是要将每个项的所有因子都放入它的factors列表，将每个表达式的所有项都放入它的terms列表，同时维护好符号关系。

递归下降通过Parser类实现Parser类具有如下属性和构造方法：

Public class Parser {
    private final Lexer lexer;
    public Parser(Lexer lexer) {
        this.lexer = lexer;
    }
}

同时为了解析表达式，项和因子，Parser类还要实现如下方法：

public Expr parseExpr() {}      // 解析表达式，返回表达式类
public Term parseTerm() {}      // 解析项，返回项类
public Factor parseFactor() {}  // 解析因子，返回因子类
public Num parseNum() {}        // 解析常数，返回常数类
public Var parseVar() {}        // 解析幂函数，返回幂函数类

这样，我们就得到了一个表达式对象，它的terms列表中维护了它所有的项，signs列表中维护了这些项的符号。

表达式展开

分析可知，本次表达式展开的最终结果是一个多项式形式：

$Expr= \sum a_ix^{i}$

多项式由一些列单项式构成，每个单项式都是$a_ix^i$的形式。因此我们构造多项式类和单项式类：

public class Poly {
    private ArrayList<Mono> monoList = new ArrayList<>();
	public Poly addPoly(Poly B) {...}   // A+B
   	public Poly subPoly(Poly B) {...}   // A-B
	public Poly mulPoly(Poly B) {...}   // A*B
	public Poly powPoly(int exp) {...}  // A^exp
}

public class Mono {
    private BigInteger coe;  // 单项式的系数
    private BigInteger exp;  // 单项式的指数
    public Poly monMulPol(Poly polyB) {...} // 单项式乘多项式
    public Mono monMulMon(Mono polyB) {...} // 单项式乘单项式
}

其中多项式类维护一个单项式列表来管理构成该多项式的所有单项式。同时多项式类还实现了加，减，乘，乘方计算的方法。单项式类实现了单项式乘多项式和单项式乘单项式的方法。此过程应当注意深浅拷贝的区别。

这样之后，我们就可以在Expr、Term、Factor等类中都写一个toPoly()方法，将类中的内容转化为多项式。然后从factor.toPoly()一步步向上转化，那么最终可以通过expr.toPoly()来获得结果。这里以expr2poly为示例：

/*Expr.java*/
Poly expr2poly() {
        Poly ret = new Poly();
        for (int i = 0; i < this.terms.size(); i++) {
            if (this.signs.get(i).getType() == Token.Type.ADD) {
                ret = ret.addPoly(this.terms.get(i).term2poly());      
            } else if (this.signs.get(i).getType() == Token.Type.SUB) {
                ret = ret.subPoly(this.terms.get(i).term2poly());
            }
        }
        return ret;
    }

第二次作业分析

思路概述

第二次作业主要需要解决三个问题，多层括号嵌套，自定义递推函数处理，三角函数处理。
对于嵌套括号，主要在parseExprFactor（解析表达式因子）方法中采用递归的方法实现。
对于自定义递推函数的处理，同样是在parser（解析）类中新增parseFuncFactor（解析自定义递推函数因子）方法实现。我们在工具类Definer中通过递归的方法进行实参替换形参，达到计算递推函数的目的。
对于三角函数，我们也要新增parseSinCosFactor（解析三角函数因子）方法进行解析。但是三角函数的重头戏是在于它改变了多项式poly的最基础组成单位（在第一次作业中，多项式的组成单位是形如$a*x^n$的单项式，但在此不是）。因此我们还需要重写poly，unit中的一系列方法。

嵌套括号

public ExprFactor parseExprFactor() {      // 解析表达式因子
    ...
    if (lexer.getCurToken().getTpye == LPAREN) { // 如果当前在解析表达式因子的过程中碰到了嵌套括号（注意这里要区分三角函数和自定义函数的括号）
        String str = parseFactor().toString(); // 递归使用parseFactor的方法解析嵌套括号中的内容
        String strSimpled = Definer.simplify(str); // simplify是一个定义在工具类Definer中的方法，它调用整个程序的逻辑对一个字符串进行化简和展开，返回一个简化后的字符串
    }
    ...
}

自定义递推函数

public Factor parseFuncFactor() {
    // eg: f{3}(x^2,x+1)
    ...
    String funcName = ... // 这里funcName指的是递归函数的层数，如：3
    paras = Definer.getParaList(sb.toString);  // 传入一个中括号包着的字符出，如：(x^2,x+1)，返回形参构成的列表
    FuncFactor func = new FuncFactor(FuncName, paras); 
    return func.retExprFactor();   // 定义于FuncFactor类中的方法，返回一个表达式因子
}

public ExprFactor retExprFactor() {
    String newFuncStr = Definer.callFunc(funcName, paras);  
    /* 这里利用工具类Definer中的callFunc方法，用实参替换掉形参，返回一个字符串，达到处理递推函数的目的
    如f{3}(x,y) = sin(x) + cos(y)，实参是(x^2,x+1)
    那么我们要返回的newFuncStr就是 sin((x^2)) + cos((x+1))
    */ 
    return new ExprFactor(1, newFuncStr);
    // 我们将结果包装为(newFuncStr)^1的形式，即达到了返回一个Factor的目的
}

三角函数

增添三角函数过后，组成多项式的基本单元（Unit）从$ax^n$变为了$ax^n\prod sin(…)\prod cos(…)$，这就要求我们修改Unit的属性和方法

public class Unit {
    private BigInteger coe;
    private BigInteger exp;
    private ArrayList<Sin> sinsInUnit = new ArrayList<>();
    private ArrayList<Cos> cossInUnit = new ArrayList<>();
}

// 对于多项式的加减法，我们直接合并两个Poly的Units列表
// 对于多项式的乘法和幂，如A*B，我们将其转化为A的所有Unit乘Poly B
// 也就是说我们要在Unit中实现：
public Poly unitMulPoly(Poly B) {
    for (Unit UnitB : B.getUnitsList()) {
        // 单项式乘单项式（unitMulUnit）
    }
} 
// 而单项式乘多项式的本质是单项式乘单项式的求和：
public Poly unitMulunit(Unit B) {
    // a*x^n1*sin(...)*cos(...) * b*x^n2*sin(...)*cos(...)
	// 直接将两个unit的sin cos列表合并，注意合并后化简，如sin(x)*sin(x)应化简为sin(x)^2
}

第三次作业分析

思路概述

第三次作业新增了自定义普通函数和求导因子两项，其中自定义普通函数的实参替换形参与自定义递推函数的处理方法相同。对于$g(x) = h(h(x))$这样的嵌套定义，我们只需类似地递归替换即可。
完成自定义函数的处理后，我们开始考虑对表达式因子的求导。由于题目明确指出只会在最后一行输入待处理的表达式中会出现求导因子，因此我们只需在parse的时候调用工具类中的求导方法，返回一个求导后的字符串，再包裹成ExprFactor的形式即可达到求导的目的，具体细节见下文。

求导因子

public Factor parseFactor() {
    ...
    if (lexer.getCurToken().getType() == Token.Type.DER) {
        return parseDerFactor();
    }
    ...
}

public Factor parseDerFacter() {
    // 处理形如 dx(x^2+2*x+1) 这样的求导因子
    String under = Derivative.Derivate(lexer);
    // 我们调用的是工具类Derivative中的Derivate方法来处理碰到dx词块的情况
    // 对于上述例子，我们期望返回的under是求导后的2*x+2，这样我们便可以把它包裹为(2*x+2)^1的表达式因子的形式作为parseDerFactor的返回值
    return new ExprFactor(1, under);
}

public static String Derivate(Lexer lexer) { // 当前词块为d 返回求完导后的字符串
        // 这里以dx(x^2+x+x+1)为例
    	... // sb.toString()是dx的括号里包裹的待求导的式子
        String inside = Definer.simplify(sb.toString()); // inside 储存利用全局方法化简后的待求导的多项式的字符串形式，在这里inside = x^2+2*x+1
    
        Lexer lexerNew = new Lexer(sb.toString());   // 词法解析
        Parser parserNew = new Parser(lexerNew);     // 解析逻辑
        Expr exprNew = parserNew.parseExpr();        // 得到解析过后的原表达式
        Poly poly = exprNew.expr2poly().merge();     // 得到dx括号里的式子的多项式形式，现在要对它求导，返回一个多项式
        Poly polyDer = poly.derivate();
        return polyDer.toString();
}

通过上述操作，我们的最终问题被转化为了：实现对标准多项式Poly的求导方法

public Poly derivate() {
    Poly polyDer;
    for (Unit unit : this.unitsList) {
            polyDer = polyDer.addPoly(unit.derivate()); // 对Poly的求导转化为对Unit的求导的和
    } 
    return polyDer;
} 

public Poly derivate() { // 对单项式求导 返回多项式
        Poly ans = new Poly();
        if (this.exp.compareTo(BigInteger.ZERO) > 0) { // 如果指数非0，对a*x^n求导
            Unit unit1 = new Unit(this.coe.multiply(this.exp), this.exp.subtract(BigInteger.ONE), this.sinsInUnit, this.cossInUnit);
            ans.addUnit2Poly(unit1);
        }
        if (!this.sinsInUnit.isEmpty()) { // 如果sin函数列表非空，对\prod sin(...)求导
            for (Sin sin : this.sinsInUnit) { 
                Unit unitTemp = this.copy();
                unitTemp.getSins().remove(sin);
                ans = ans.addPoly(unitTemp.unitMulPol(sin.derivate()));
            }
        }
        if (!this.cossInUnit.isEmpty()) {
            for (Cos cos : this.cossInUnit) {
            	...  // 类似sin
            }
        }
        return ans.merge();
    }

回首上述过程，我们对表达式的求导被一层层地拆解为一个个更简单的目标：从对表达式求导到对poly求导，再到对sin和cos求导，再到对x和常数的求导。我们在事实上实现了层次化求导的构建。

架构设计体验

在我的设计中，第一次作业的架构主要参考了oopre_hw7的解析下降架构，即：利用lexer划分词块。再利用parser完成对Expr，Term，Factor的三级构建。接着再利用toPoly方法将上述三级转化为标准的多项式，在转化的过程中事实上就进行了表达式计算。最后输出exprToPoly的结果即可。

第二次和第三次开发在第一次的架构上并未大改，究其原因：我们新增的自定义递推函数，自定义普通函数，三角函数在某种程度上都可以看成一种“因子”，我们只需新增几个Factor接口的实现即可。而且它们经过parse后返回的结果都是一个表达式，我们将其包裹为表达式因子的形式便可轻松与第一次设计的架构完美接轨。

如果还要新增加迭代，例如实现求和函数，甚至定积分等，理论上都可以通过方法类处理返回表达式 + 包裹为表达式因子的方法接入我们的架构。这决定了我们以后的每次增量开发都只需要专心于新的问题的特性，而无需过多考虑如何融入架构进行共性处理。

这说明了一个灵活的，包容的架构的重要性，这也是架构设计的魅力所在。

BUG分析

本单元作业我在第二，三次作业中分别出现了一次bug，

第二次作业的bug出在获取参数列表上，getParaList()函数获取一个括号包裹的字符串，返回括号中的实参。如：输入字符串为(x^2, x+1)，输出实参列表包含x^2, x+1两项。在最初的实现中，把逗号作为一个实参和另一个实参的区分，即碰到逗号便截断为一个实参。

这忽略了如下情况：f{2}(x, f{0}(1,2))。通过限制截断时左括号与右括号数相差1的条件可以在一行内解决该问题。修改前后复杂度改变可忽略不计。

第三次作业的bug出在自定义普通函数在嵌套时进行替换后的式子未加括号，导致识别错误。实例如下：

2
h(x) = +6*+1
g(x) = sin(x)
0
g(h(1))

最初的实现中，函数g的实参替换完形参x后的结果如下，sin(+6*+1)这不符合我们要求三角函数内部是因子的限制，因而自然地不能得到正确答案，通过增加括号包裹替换完的结果能在一行内解决上述问题，得到sin((+6*+1))这样可以正确处理的式子。修改所带来的复杂度改变同样可以忽略不计。

关于互测，我一般利用自己在设计和检查考虑到的容易错的情况来构造数据，比较有效。在第一次作业写了测评机的情况下有针对被测程序的代码来构造用例。

上述两个错误均属于极其细微且不容易通过手动构造样例检查出的。这也与我第二，三次作业未写测评机有关。这启示我们构造自动化测试来检验程序的正确性。

心得体会

1. 在第一次作业中建立灵活的，包容性强的架构。尽可能使得增量开发只需要专注与增量的特性而不需过多的考虑共性问题。
1. 构造自动化测试工具检查程序正确性。
1. 尽可能提取方法，降低单个方法的复杂度，以增加可读性和避免出错。
1. 未来第一单元的课程可以平衡一下第二，三次作业的难度梯度。

[BUAA-OO] 第一单元：表达式展开

概述

UML类图和度量分析

第一次作业分析

思路概述

语法解析（递归下降）

表达式展开

第二次作业分析

思路概述

嵌套括号

自定义递推函数

三角函数

第三次作业分析

思路概述

求导因子

架构设计体验

BUG分析

心得体会

[`BUAA-OO`] 第一单元：表达式展开

`UML`类图和度量分析